$n$ adet noktasal yükün kuvveti¶

$n$ adet noktasal yükün bir noktasal yüke uyguladıkları toplam kuvvetin ifadesi aşağıdaki gibi yazılır.

Süperpozisyon

$$\mathbf{F}_T=\frac{q_1q}{4\pi\varepsilon_0 D_1^2}\mathbf{a}_{D_1}+\frac{q_2q}{4\pi\varepsilon_0 D_2^2}\mathbf{a}_{D_2}+\cdots +\frac{q_nq}{4\pi\varepsilon_0 D_n^2}\mathbf{a}_{D_n}$$ $$\mathbf{F}_T=\dfrac{q}{4\pi\varepsilon_0}\sum_{i=1}^n \dfrac{q_i}{D_i^2}\mathbf{a}_{D_i}$$

Uygulama 1¶

İki adet noktasal yükün tek yüke uyguladıkları kuvvet

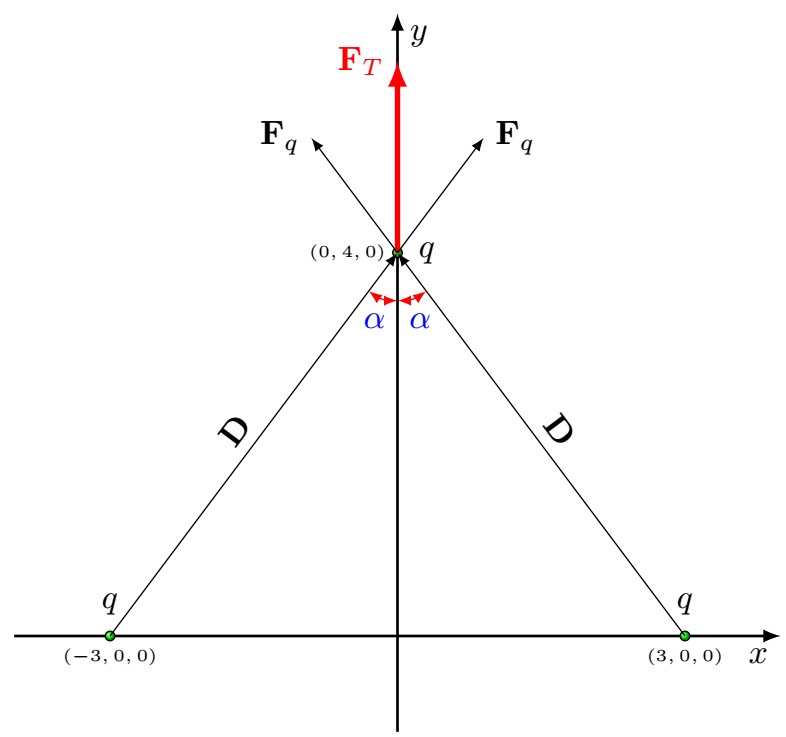
Kartezyen koordinat sisteminde $P_1(3,0,0)$ ve $P_2(-3,0,0)$ noktalarına yerleştirilmiş $q$ değerlikli noktasal yüklerin $P(0,4,0)$ noktasına yerleştirilmiş $q$ noktasal yüküne uyguladıkları toplam kuvveti hesaplayınız.

Çözüm:

$$\mathbf{F}_T=2×\frac{q\ q}{4\pi\varepsilon_0 D^2}\cos \alpha\ \mathbf{a}_y$$ $$D= \sqrt{3^2+4^2}=5,\, \cos α=\frac{4}{5}$$ $$\mathbf{F}_T=\dfrac{72\ q^2}{125}\times 10^{9}\ \mathbf{a}_y\quad \text{(N)} $$

Python Kod:

import numpy as np
from numpy import linalg as LA

eps0 = 1E-9/(36 * np.pi)
Q1, Q2, Q3 = 1E-9, 1E-9, 1E-9 #Noktasal Yüklerin Değerleri
Q1P = [3,0,0]
Q2P = [-3,0,0]
Q3P = [0,4,0]
D1 = np.subtract(Q3P,Q1P)
D2 = np.subtract(Q3P,Q2P)
D_gen_1 = LA.norm(D1)
D_gen_2 = LA.norm(D2)
F1 = (Q1 * Q3 * D1) / (4*np.pi*eps0*D_gen_1**3) 
F2 = (Q2 * Q3 * D2) / (4*np.pi*eps0*D_gen_2**3) 
F_T = F1 + F2
print("$F_T=$ ", F_T[0],"ax",F_T[1],"ay",F_T[2],"az")

$F_T=$ 0.0 ax 5.76e-10 ay 0.0 az (N)

\(n\) adet noktasal yükün kuvveti¶

Uygulama 1¶