Yük Kavramı¶
Yük Kavramı¶
Elektromanyetik alanların temel fiziksel büyüklüğü elektrik yükleridir. Bütün elektromanyetik alanların kaynağı olan yükün birimi Coulomb (C)’dur. Bir elektron bilinen en küçük değerdeki yüktür ve değeri yaklaşık olarak \(-1.6\times 10^{-19}\ (C)\)'dur. Elektron negatif değerlikli yük kaynağı iken, proton ise pozitif değerli yük kaynağıdır ve yük değeri \(1.6\times 10^{-19}\ (C)\)'dur.
Alan kaynağı olan yüklerimiz, uzayın bir noktasında izole şekilde bulunabilirler. Bunun yanında çizgisel, yüzeysel ya da hacimsel olarak bir dağılım gösterebilirler. Statik elektrik alanların temel kanunu olan Coulomb kanunu, iki noktasal yükün birbirlerine uyguladığı kuvvetin değerini verir. Eğer yüklerimiz bir dağılım şeklinde bulunuyorsa, mesela kuvvet değerini hesaplayabilmemiz için diferansiyel bir yaklaşım uygulamamız gerekecektir. Aynı zamanda problem geometrisine uygun koordinat sistemini seçmemiz ve diferansiyel büyüklüklerimiz bu koordinat sistemine göre oluşturmalıyız.
Toplam Yük Hesabı¶
Çizgisel, yüzeysel ve hacimsel yük dağılımlarının oluşturdukları toplam yük değerleri aşağıdaki gibi hesaplanır.
Toplam Yük Değeri Hesabı
\begin{align} Q &=\int_l \lambda\ d\mathbf{\ell}\nonumber \\ Q &=\int_s \sigma\ ds\\ Q &=\int_v \rho\ dv \nonumber \end{align}
\(\lambda\ (\small C/m)\) çizgisel, \(\sigma\ (\small C/m^2)\) yüzeysel, \(\rho\ (\small C/m^3)\) hacimsel yük yoğunluğunu göstermektedir.
Uygulama 1¶
Toplam Yük Değeri Hesabı
$x^2+y^2=16$ çemberi üzerinde $5 (\small nC/m)$'lik yük yoğunluğu vardır. Toplam yük değerini hesaplayınız.
Çözüm:
$$Q = \int_l \lambda\ \mathrm{d}l$$ $$\mathrm{d}l=r \mathrm{d}\phi$$ $$Q=r\lambda\int_l \mathrm{d}\phi=r\lambda \int_0^{2\pi}\ \mathrm{d}\phi=4\times 5\times 10^{-9} \Big| \phi \Big|_0^{2\pi}=400\pi 10^{-9} (C)$$
Uygulama 2¶
Toplam Yük Değeri Hesabı
Yarıçapı $a$ olan disk üzerindeki yük yoğunluğu, merkezinden itibaren $k$ orantı katsayısı ile lineer olarak artmaktadır. Disk üzerindeki toplam yük miktarını hesaplayınız.
Çözüm:
\begin{align} Q&=\int_s \sigma\ ds=\int_s \sigma\ rd\phi dr\\ Q&=\int\limits_{r=0}^a \int\limits_{\phi=0}^{2\pi} kr\ rd\phi dr\\ Q&=\frac{2}{3}\pi ka^3\ (C) \end{align}
Uygulama 3¶
Toplam Yük Değeri Hesabı
Yarıçapı $a$ olan küre içindeki yük yoğunluğu $\rho=\dfrac{1}{R^2\sin \theta} (C/m^3)$ olarak tanımlanmıştır. Küredeki toplam yük miktarını hesaplayınız.
Çözüm:
\begin{align} Q&=\int_v \rho\ dv=\int_s \rho\ R^2\sin \theta\ d\theta\ d\phi\ dR\\ Q&=\int_{0}^{a} \!\! \int_{0}^{\pi} \!\! \int_{0}^{2\pi} \dfrac{1}{R^2\sin \theta}\ R^2\sin \theta\ d\theta\ d\phi\ dR \\ Q&=2 a \pi^2\ (C) \end{align}
Uygulama 4¶
Toplam Yük Değeri Hesabı
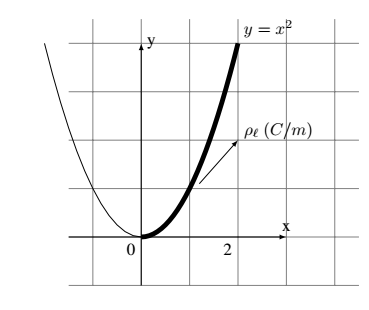
$y=x^2$ parabolü üzerinde $\lambda = 5\, \text{(nC/m)} $'lik yük yoğunluğu vardır. $0\leq x \leq 2 $ aralığındaki toplam yük değerini hesaplayınız.
Çözüm: