Yük Dağılımları¶

Çizgisel yük dağılımı

$$\mathbf{E}=\int_l \dfrac{\lambda\ \mathrm{d}\mathbf{l}}{4\pi\varepsilon_0 D^2}\mathbf{a}_D $$

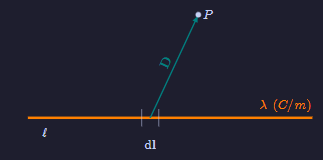
Uygulama

Sonsuz uzun çizgisel yük dağılımı $x$ ekseni boyunca yerleşik ve üzerinde $\lambda\ \text{(C/m)}$'lik yük yoğunluğu vardır. $(0,d,0)$ noktasında oluşan elektrik alan şiddeti vektörünü hesaplayınız.

---

Çözüm:
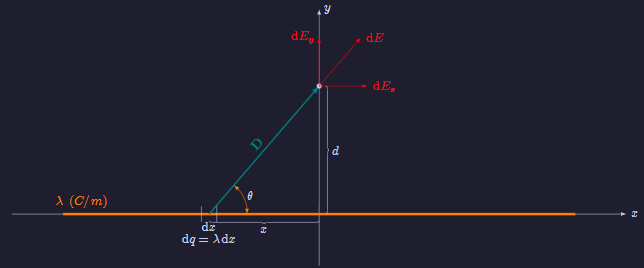$$dE=\frac {dq} {4πϵ_0D^2} e^{jθ}=\frac {λdx} {4πϵ_0(d^2+x^2)} e^{jθ}$$ $$ \begin{align} dE=dE_x+jdE_y \nonumber \\ dE_x=\frac {λdx} {4πϵ_0(d^2+x^2)} \cosθ \nonumber \\ dE_y=\frac {λdx} {4πϵ_0(d^2+x^2)} \sinθ \nonumber \end{align} $$ $$E=∫^∞_{−∞} \frac {λ} {4πϵ_0(d^2+x^2)} [\cosθ+j\sinθ]dx $$ $$\cosθ=\frac {x} {(x^2+d^2)^{1/2}} ; \sinθ=\frac {d} {(x^2+d^2)^{1/2}} $$ $$ \begin{align} E&=jE_y=j∫^∞_{−∞} \frac {λd} {4πϵ_0} \frac {dx} {(x^2+d^2)^{3/2}} \\ &=j\frac {λd} {4πϵ_0} \Bigg[\frac {x} {d^2(x^2+d^2)^{1/2}}\Bigg]^∞_{−∞} \\ &=j\frac {λd} {4πϵ_0} \Bigg[\frac 1 {d^2} + \frac 1 {d^2}\Bigg] = j\frac {λ} {2πϵ_0d} \\ E&=\frac λ {2πϵ_0d}\ \text{(V/m)} \nonumber \end{align} $$

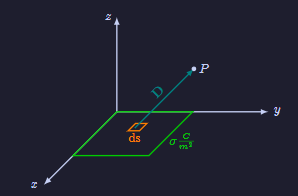
Yüzeysel yük dağılımı

$$\mathbf{E}=\int_S \dfrac{\sigma\ \mathrm{d}\mathbf{s}}{4\pi\varepsilon_0 D^2}\mathbf{a}_D $$

Hacimsel yük dağılımı

$$\mathbf{E}=\int_v \dfrac{\rho\ \mathrm{d}v}{4\pi\varepsilon_0 D^2}\mathbf{a}_D $$